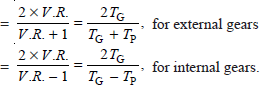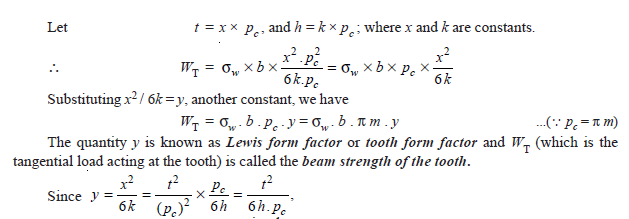Wear tooth load

Machine Design

Gear Drive

Wear tooth load

Introduction:

The maximum load that gear teeth can carry, without premature wear, depends upon the radii of curvature of the tooth profiles and on the elasticity and surface fatigue limits of the materials.

Calculations:

The maximum or the limiting load for satisfactory wear of gear teeth, is obtained by using the following Buckingham equation, i.e

W_w = D_P.b.Q.K

where

W_w = Maximum or limiting load for wear in newtons,
D_P = Pitch circle diameter of the pinion in mm,
b = Face width of the pinion in mm,
Q = Ratio factor

V.R. = Velocity ratio = TG / TP,
K = Load-stress factor (also known as material combination factor) in N/mm².

The load stress factor depends upon the maximum fatigue limit of compressive stress, the pressure angle and the modulus of elasticity of the materials of the gears. According to Buckingham, the load stress factor is given by the following relation :

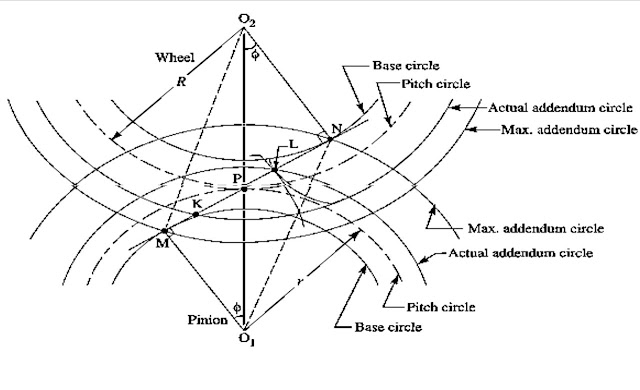
where σ_es = Surface endurance limit in MPa or N/mm²,
φ = Pressure angle,
E_P = Young's modulus for the material of the pinion in N/mm², and
E_G = Young's modulus for the material of the gear in N/mm².

Notes :

1. The surface endurance limit for steel may be obtained from the following equation : σ_es = (2.8 × B.H.N. – 70) N/mm²
2. The maximum limiting wear load (W_w) must be greater than the dynamic load (W_D).

Static tooth load

Machine Design

Gear Drive

Static tooth load

Introduction:

The static tooth load (also called beam strength or endurance strength of the tooth) is obtained by Lewis formula by substituting flexural endurance limit or elastic limit stress (σ_e) in place of permissible working stress (σ_w).

Static Tooth Load

∴ Static tooth load or beam strength of the tooth,

W_S = σ_e.b.p_c.y = σ_e.b.π m.y

Values of flexural endurance limit

For safety, against tooth breakage, the static tooth load (W_S) should be greater than the dynamic load (W_D). Buckingham suggests the following relationship between W_S and W_D.

For steady loads,

WS ≥ 1.25 WD
For pulsating loads,

WS ≥ 1.35 WD
For shock loads,

WS ≥ 1.5 WD

Note : For steel, the flexural endurance limit (σe) may be obtained by using the following relation :

σ_e = 1.75 × B.H.N. (in MPa)

Dynamic load on gear

Machine Design

Gear Drive

Dynamic load on gear

Introduction:

The velocity factor was used to make approximate allowance for the effect of dynamic loading.

Reasons of dynamic load:

The dynamic loads are due to the following reasons :

1. Inaccuracies of tooth spacing,
2. Irregularities in tooth profiles, and
3. Deflections of teeth under load.

A closer approximation to the actual conditions may be made by the use of equations based on extensive series of tests, as follows :

WD = WT WI

where WD = Total dynamic load,
WT = Steady load due to transmitted torque, and
WI = Increment load due to dynamic action.
The increment load (WI) depends upon the pitch line velocity, the face width, material of the gears, the accuracy of cut and the tangential load. For average conditions, the dynamic load is determined by using the following Buckingham equation, i.e.

where
WD = Total dynamic load in newtons,
WT = Steady transmitted load in newtons,
v = Pitch line velocity in m/s,
b = Face width of gears in mm, and
C = A deformation or dynamic factor in N/mm.

A deformation factor (C) depends upon the error in action between teeth, the class of cut of the gears, the tooth form and the material of the gears. The following table shows the values of deformation factor (C) for checking the dynamic load on gears.

The value of C in N/mm may be determined by using the following relation :

where K = A factor depending upon the form of the teeth.
              = 0.107, for 14 1/2 ° full depth involute system.
              = 0.111, for 20° full depth involute system.
              = 0.115 for 20° stub system.
EP = Young's modulus for the material of the pinion in N/mm2.
EG = Young's modulus for the material of gear in N/mm2.
e = Tooth error action in mm.

The maximum allowable tooth error in action (e) depends upon the pitch line velocity (v) and the class of cut of the gears

Permissible Working Stress for Gear Teeth

Introduction:
The allowable static stress is the stress at the elastic limit of the material.
Permissible Working Stress for Gear Teeth

• The permissible working stress (σw) in the Lewis equation depends upon the material for which an allowable static stress (σo) may be determined.
• The allowable static stress is the stress at the elastic limit of the material. It is also called the basic stress. In order to account for the dynamic effects which become more severe as the pitch line velocity increases, the value of σw is reduced.

According to the Barth formula, the permissible working stress,

σw = σo × Cv

where
σo = Allowable static stress, and
Cv = Velocity factor.

The values of the velocity factor (Cv) are given as follows :

The following table shows the values of allowable static stresses for the different gear materials.

Note : The allowable static stress (σo) for steel gears is approximately one-third of the ultimate tensile stregth (σu) i.e. σo = σu / 3.

Machine Drives ( Gear Drives ) (The beam strength of gear teeth)

Machine Design

Gear Drive

The beam strength of gear teeth

Introduction:

The beam strength of gear teeth is determined from an equation (known as *Lewis equation) and the load carrying ability of the toothed gears as determined by this equation gives satisfactory results.

Lewis Equation

• Lewis assumed that as the load is being transmitted from one gear to another, it is all given and taken by one tooth, because it is not always safe to assume that the load is distributed among several teeth.
• When contact begins, the load is assumed to be at the end of the driven teeth and as contact ceases, it is at the end of the driving teeth. This may not be true when the number of teeth in a pair of mating gears is large, because the load may be distributed among several teeth.

Consider each tooth as a cantilever beam loaded by a normal load (WN) . It is resolved into two components i.e. tangential component (WT) and radial

component (WR) acting perpendicular and parallel to the centre line of the tooth respectively. The tangential component (WT) induces a bending stress which tends to break the tooth. The radial component (WR) induces a compressive stress of relatively small magnitude, therefore its effect on the tooth may be neglected. Hence, the bending stress is used as the basis for design calculations. The critical section or the section of maximum bending stress may be obtained by drawing a parabola through A and tangential to the tooth curves at B and C. This parabola outlines a beam of uniform strength, i.e. if the teeth are shaped like a parabola, it will have the same stress at all the sections. But the tooth is larger than the parabola at every section except BC.The section BC is the section of maximum stress or the critical section. The maximum value of the bending stress (or the permissible working stress), at the section BC is given by

  σw = M.y / I                         ...(i)
where M = Maximum bending moment at the critical section BC = WT × h,
WT = Tangential load acting at the tooth,
h = Length of the tooth,
y = Half the thickness of the tooth (t) at critical section BC = t/2,
I = Moment of inertia about the centre line of the tooth = b.t3/12,
b = Width of gear face.
Substituting the  values for M, y and I in equation (i), we get

In this expression, t and h are variables depending upon the size of the tooth (i.e. the circular pitch) and its profile.

The value of y in terms of the number of teeth may be expressed as follows :

Machine Drives ( Gear Drives ) (Gear material)

Machine Design

Gear Drive

Gear material

Introduction:
The material used for the manufacture of gears depends upon the strength and service conditions like wear, noise etc. The gears may be manufactured from metallic or non-metallic materials.
Properties of commonly used gear materials

• The metallic gears with cut teeth are commercially obtainable in cast iron, steel and bronze. The nonmetallic materials like wood, rawhide, compressed paper and synthetic resins like nylon are used for gears, especially for reducing noise.
• The cast iron is widely used for the manufacture of gears due to its good wearing properties, excellent machinability and ease of producing complicated shapes by casting method. The cast iron gears with cut teeth may be employed, where smooth action is not important.
• The steel is used for high strength gears and steel may be plain carbon steel or alloy steel. The steel gears are usually heat treated in order to combine properly the toughness and tooth hardness.

The phosphor bronze is widely used for worm gears in order to reduce wear of the worms which will be excessive with cast iron or steel. The following table shows the properties of commonly used gear materials.

Machine Drives ( Gear Drives ) (Minimum number of teeth on the pinion in order to avoid interference)

Machine Design

Gear Drive

Minimum number of teeth on the pinion in order to avoid interference

Introduction:
Interference may only be avoided, if the point of contact between the two teeth is always on the involute profiles of both the teeth.
Minimum number of teeth on the pinion in order to avoid interference

The minimum number of teeth on the pinion which will mesh with any gear (also rack) without interference are given in the following table.

The number of teeth on the pinion (TP) in order to avoid interference may be obtained from the following relation :
where

AW = Fraction by which the standard addendum for the wheel should be multiplied,

G = Gear ratio or velocity ratio = TG / TP = DG / DP,

φ = Pressure angle or angle of obliquity.

Machine Drives ( Gear Drives ) (14) (Interference in Involute gear)

Machine Design

Gear Drive

Interference in Involute gear

Introduction:

The phenomenon when the tip of a tooth undercuts the root on its mating gear is known as interference.

Interference in involute gears

• MN is the common tangent to the base circles and KL is the path of contact between the two mating teeth.
• If the radius of the addendum circle of pinion is increased to O1N, the point of contact L will move from L to N. When this radius is further increased, the point of contact L will be on the inside of base circle of wheel and not on the involute profile of tooth on wheel.
• The tip of tooth on the pinion will then undercut the tooth on the wheel at the root and remove part of the involute profile of tooth on the wheel. This effect is known as interference and occurs when the teeth are being cut.
• In brief, the phenomenon when the tip of a tooth undercuts the root on its mating gear is known as interference. Similarly, if the radius of the addendum circle of the wheel increases beyond O2M, then the tip of tooth on wheel will cause interference with the tooth on pinion.
• The points M and N are called interference points. Obviously interference may be avoided if the path of contact does not extend beyond interference points.
• The limiting value of the radius of the addendum circle of the pinion is O1N and of the wheel is O2M.
• The interference may only be avoided, if the point of contact between the two teeth is always on the involute profiles of both the teeth. In other words, interference may only be prevented, if the addendum circles of the two mating gears cut the common tangent to the base circles between the points of tangency.

Note :
In order to avoid interference, the limiting value of the radius of the addendum circle of the pinion (O1 N) and of the wheel (O2 M), may be obtained as follows

Machine Drives ( Gear Drives ) (13) ( Comparision between involute and cycloidal gear)

Machine Design

Gear Drive

Introduction:

The involute gears are more commonly used as compared to cycloidal gears.

Advantages of involute gears

1. The most important advantage of the involute gears is that the centre distance for a pair of involute gears can be varied within limits without changing the velocity ratio. This is not true for cycloidal gears which requires exact centre distance to be maintained.

2. In involute gears, the pressure angle, from the start of the engagement of teeth to the end of the engagement, remains constant. It is necessary for smooth running and less wear of gears. But in cycloidal gears, the pressure angle is maximum at the beginning of engagement, reduces to zero at pitch point, starts increasing and again becomes maximum at the end of engagement. This results in less smooth running of gears.

3. The face and flank of involute teeth are generated by a single curve whereas in cycloidal gears, double curves (i.e. epicycloid and hypocycloid) are required for the face and flank respectively.
Thus the involute teeth are easy to manufacture than cycloidal teeth. In involute system, the basic rack has straight teeth and the same can be cut with simple tools.

Note : The only disadvantage of the involute teeth is that the interference occurs with pinions having smaller number of teeth. This may be avoided by altering the heights of addendum and dedendum of the mating teeth or the angle of obliquity of the teeth.

Advantages of cycloidal gears

Following are the advantages of cycloidal gears :

1. Since the cycloidal teeth have wider flanks, therefore the cycloidal gears are stronger than the involute gears for the same pitch. Due to this reason, the cycloidal teeth are preferred specially for cast teeth.

2. In cycloidal gears, the contact takes place between a convex flank and concave surface, whereas in involute gears, the convex surfaces are in contact. This condition results in less wear in
cycloidal gears as compared to involute gears. However the difference in wear is negligible.

3. In cycloidal gears, the interference does not occur at all. Though there are advantages of cycloidal gears but they are outweighed by the greater simplicity and flexibility of the involute gears.

Machine Design (Gear Drives) (12) (Involute Teeth)

Machine Design

Gear Drive

Involute Teeth

Introduction:

An involute of a circle is a plane curve generated by a point on a tangent, which rolls on the circle without slipping or by a point on a taut string which is unwrapped from a reel.
Construction of involute teeth

Let A be the starting point of the involute.
The base circle is divided into equal number of parts e.g. AP1, P1 P2, P2 P3 etc.The tangents at P1, P2, P3 etc., are drawn and the lenghts P1A1, P2A2, P3A3 equal to the arcs AP1, AP2 and AP3 are set off.
Joining the points A, A1, A2, A3 etc., we obtain the involute curve AR. At any instant A3, the tangent A3T to the involute is perpendicular to P3A3 and P3A3 is the normal to the involute.

In other words, normal at any point of an involute is a tangent to the circle. Now, let O1 and O2 be the fixed centres of the two base circles as shown in Fig.(b).
Let the corresponding involutes AB and A'B' be in contact at point Q. MQ and NQ are normals to the involute at Q and are tangents to base circles.

Since the normal for an involute at a given point is the tangent drawn from that point to the base circle, therefore the common normal MN at Q is also the common tangent to the two base circles.

The common normal MN intersects the line of centres O1O2 at the fixed point P (called pitch point). Therefore the involute teeth satisfy the fundamental condition of constant velocity ratio.

From similar triangles O2 NP and O1 MP,
which determines the ratio of the radii of the two base circles. The radii of the base circles is given by

O1M = O1 P cos φ, and O2N = O2 P cos φ

where φ is the pressure angle or the angle of obliquity.
Also the centre distance between the base circles

If the centre distance is changed, then the radii of pitch circles also changes. But their ratio remains unchanged, because it is equal to the ratio of the two radii of the base circles. The common normal, at the point of contact, still passes through the pitch point. As a result of this, the wheel continues to work correctly. However, the pressure angle increases with the increase in centre distance.

Machine Design ( Gear Drive) (11) (cycloidal teeth)

Machine Design

Gear Drive

Cycloidal teeth

Introduction:
A cycloid is the curve traced by a point on the circumference of a circle which rolls without slipping on a fixed straight line.
Cycloidal Teeth
A cycloid is the curve traced by a point on the circumference of a circle which rolls without slipping on a fixed straight line.When a circle rolls without slipping on the outside of a fixed circle, the curve traced by a point on the circumference of a circle is known as epicycloid.On the other hand, if a circle rolls without slipping on the inside of a fixed circle, then the curve traced by a point on the circumference of a circle is called hypocycloid

the fixed line or pitch line of a rack is shown.When the circle C rolls without slipping above the pitch line in the direction as indicated, then the point P on the circle traces the epicycloid PA. This represents the face of the cycloidal tooth profile.When the circle D rolls without slipping below the pitch line, then the point P on the circle D traces hypocycloid PB which represents the flank of the cycloidal tooth. The profile BPA is one side of the cycloidal rack tooth.Similarly, the two curves P' A' and P' B' forming the opposite side of the tooth profile are traced by the point P' when the circles C and D roll in the opposite directions. In the similar way, the cycloidal teeth of a gear may be constructed as shown.The circle C is rolled without slipping on the outside of the pitch circle and the point P on the circle C traces epicycloid PA, which represents the face of the cycloidal tooth.The circle D is rolled on the inside of pitch circle and the point P on the circle D traces hypocycloid PB, which represents the flank of the tooth profile.The profile BPA is one side of the cycloidal tooth. The opposite side of the tooth is traced as explained above.

Construction of two mating cycloidal teeth

A point on the circle D will trace the flank of the tooth T1 when circle D rolls without slipping on the inside of pitch circle of wheel 1 and face of tooth T2 when the circle D rolls without slipping on the outside of pitch circle of wheel 2.Similarly, a point on the circle C will trace the face of tooth T1 and flank of tooth T2.The rolling circles C and D may have unequal diameters, but if several wheels are to be interchangeable, they must have rolling circles of equal diameters.The common normal XX at the point of contact between two cycloidal teeth always passes through the pitch point, which is the fundamental condition for a constant velocity ratio.

Machine Design (Factors Consider During Machine Design )

Factors to be considered during Machine Design :

When the designer designs the elements of the machine or the complete machine, they have to consider several important parameters. Here are some of the important factors to be considered while doing machine design.

●      When the designer designs the elements of the machine or the complete machine, they have to consider several important parameters. Here are some of the important factors to be considered while doing machine design:

1.  Cost: Cost has always been the major factor of consideration while designing the machine elements or machine and in this age of competition it has become more important. The best machine design is the one which helps get the finished product with all the major functionalities and highest possible quality at the lowest possible cost. Gone are the days when expensive and bulky materials were used for making the machine elements.
2. High output and efficiency: Earlier machines used to be very heavy and consume lots of power. Now the trend is of full functional machines consuming low power and giving high output in terms of the number of the of products manufactured. Some computer controlled machines can manufacture the components very fast and are highly efficient.
3. Strength: The machine elements or the machine should be strong enough to sustain all the forces it is designed for so that it is not damaged or permanently deformed during its life time. Right at the time of the designing the machine the designer should consider the force machine can be applied to and consider all the relevant factors that could affects its life.
4. Stiffness or rigidity: The machine should be rigid enough so that under the effect of applied forces for which it is designed there is no deformation of the machine or machine elements beyond the specified limits. If there is excessive deformation, there are chances of the failure of the machine elements and the whole machine.
5. Wear resistance: Wear is the removal of the material from the metallic surface when two surfaces rub with each other. If there is more removal of the material, the component will become weaker and eventually break. The wear of the contacting surfaces can be reduced by the lubrication of the surfaces, increasing the strength or the hardness of the working surfaces. The effect of wear can also be reduce by increasing the surface, so that during the lifetime of the mating machine elements they will not fail even if there is some wearing between them.
6. Lubrication: Lubrication between the two mating surfaces of the elements of the machine help reducing friction between them and wearing of the two surfaces, which results in the increase in life of the components of the machine.
7. Operational safety: For the safety of the operator of the machine, the hazard producing things from the machine should be eliminated and the design should confirm to the safety codes.
8. Ease of assembly: The elements of the machine should be such that the machine can be assembled very easily. For the mass production of the complex machines like automobiles, type writers etc, the concept of unit assemblies are common. The unit assemblies are assembled together to form the complete machine.
9. Ease and simplicity of disassembly: Like assembly, the disassembly of the machine also should be easy so as to easily carry out replacement of the parts, and repair and maintenance of the machine and machine elements.
10. Ease and simplicity of servicing and control: The machine and its element should be simple enough so that very little maintenance and servicing is required. The repair and maintenance of the machine should be easy and cheap and simple replacements should be available.
11. Light weight and minimum dimensions: The machine elements and machine should be strong, rigid and wear resistant with minimum weight and least dimensions. This can be achieved by using light weight rolled sections and hardening the metals. Using high strength grades of cast iron and light alloys can further help getting light materials and minimum dimensions of the machine elements. Improving the design in this direction is very important.
12. Reliability: The reliability of the machine is a very important if the machine has to find the huge market in the business.
13. Durability: The longer the life of the machine more it develops the reputation of being the dependable machine and more will be its sale. Hence the right at the time of designing reliability and durability should be given priority. For this the machine should be designed for least maintenance requirements and long-life.
14. Economy of performance: For the proper economic performance of the machine correct mechanical, hydraulic, thermodynamic and other principles should be applied while designing the elements of the machine and the whole machine.
15. Accessibility: The machine elements and machine the whole should be easy to handle and access.
16. Processability: The shape and the materials for the elements of the machine should be such that they can the processing costs and labor costs are lowest possible.
17. Compliance with state standards: Following the standards makes designing easier and availability of various parts faster and easier.
18. Economy of repairs and maintenance: While designing the machine elements and machine the designing should be such that least amount of repairs and maintenance will be required for the machine.
19. Use of standard parts: There should be maximum possible standard parts in the design of the machine. This will help reduce the cost of the machine and ensure easy availability of the parts. With standard parts the design can be modified easily.
20. Use of easily available materials: Materials selected for the machine elements during the design should be available easily and lowest possible costs.
21. Appearance of the machine: While designing the machine the aesthetics and ergonomics of the machine should be given due consideration without affecting its functionality.
22. Number of machines to be built: Designing of the machine will depend a lot on the number of machines to be manufactured. If few numbers of machines are to be manufactured then expensive materials and high production costs can be considered, but for the mass production economy of the machine should be top priority.

Machine Design (Gear) (10)

Machine Design

Gear Drive

Machine Design ( Gear Drive) (9)

Machine Design

Gear Drive

Law Of Gearing : The law of gearing states that " the common normal to the tooth profile at the point of contact should always pass through a fixed point called pitch point in order to get constant velocity ratio."

Gear Tooth Failures :
There are two basic modes of gear tooth failure : 

(a) Breakage of tooth due to static and dynamic loads. 
(b) Surface destruction. 

The complete breakage of the tooth can be avoided by adjusting the module and face width, so that the beam strength of the gear tooth is more than the sum of static and dynamic load. 

The surface destruction or tooth wear is classified as follows : 

(i) Abrasive wear : Foreign particles such as dirt, rust etc. can scratch the tooth surface. Remedies against this type of wear or provision of oil filters, increasing surface hardness and use of high viscosity oils. 

(ii) Corrosive wear : The corrosion of the tooth surface is caused by corrosive elements such as extreme pressure additives present in the lubricating oils and foreign materials due to external contamination. These elements attack the tooth surface, resulting in fine wear uniformly distributed over the entire surface. 

(iii) Initial pitting : The initial pitting is a localized phenomenon characterized by small pits at high spots. Initial pitting is caused by the errors in the tooth profile, surface irregulation and misalignment. The remedies against initial pitting are precise matching of gears, adjusting the correct alignment of gears so that the load is uniformly distributed. 

(iv) Destructive pitting : Destructive pitting is a surface fatigue failure which occurs when the load on the gear teeth exceeds the surface endurance strength of the material. This type of failure can be avoided by designing the gear in such a way that the wear strength of the gear tooth is more than the sum of static and dynamic load. 

(v) Scoring: Exclusive surface pressure, high surface speed and in adequate supply of lubrication result in the breakdown of the oil film. This results in excessive frictional heat and overheating of meshing teeth. It can be avoided by selecting the parameters such as surface speed, surface pressure and the flow of lubricant in such a way that the resulting temperature at the contacting surfaces is within permissible limit. 

Machine Design (Gear Drive) (8)

Machine Design

Gear Drive

Terminologies Of Spur Gear :

• Pitch surface : The surface of the imaginary rolling cylinder (cone, etc.) that the toothed gear may be considered to replace.
• 
  
• Pitch circle: A right section of the pitch surface.
• 
  
• Addendum circle: A circle bounding the ends of the teeth, in a right section of the gear.
• 
  
• Root (or dedendum) circle: The circle bounding the spaces between the teeth, in a right section of the gear.
• 
  
• Addendum: The radial distance between the pitch circle and the addendum circle.
• 
  
• Dedendum: The radial distance between the pitch circle and the root circle.
• 
  
• Clearance: The difference between the dedendum of one gear and the addendum of the mating gear.
• 
  
• Face of a tooth: That part of the tooth surface lying outside the pitch surface.
• 
  
• Flank of a tooth: The part of the tooth surface lying inside the pitch surface.
• 
  
• Circular thickness (also called the tooth thickness) : The thickness of the tooth measured on the pitch circle. It is the length of an arc and not the length of a straight line.
• 
  
• Tooth space: The distance between adjacent teeth measured on the pitch circle.
• 
  
• Backlash: The difference between the circle thickness of one gear and the tooth space of the mating gear.

Backlash =Space width – Tooth thickness

• 
  
• Circular pitch p: The width of a tooth and a space, measured on the pitch circle.
• 
  
• Diametral pitch P: The number of teeth of a gear per inch of its pitch diameter. A toothed gear must have an integral number of teeth. The circular pitch, therefore, equals the pitch circumference divided by the number of teeth. The diametral pitch is, by definition, the number of teeth divided by the pitch diameter.
• 
  
• Module m: Pitch diameter divided by number of teeth. The pitch diameter is usually specified in inches or millimeters; in the former case the module is the inverse of diametral pitch.
• 
  
• Fillet : The small radius that connects the profile of a tooth to the root circle.
• 
  
• Pinion: The smaller of any pair of mating gears. The larger of the pair is called simply the gear.
• 
  
• Velocity ratio: The ratio of the number of revolutions of the driving (or input) gear to the number of revolutions of the driven (or output) gear, in a unit of time.
• 
  
• Pitch point: The point of tangency of the pitch circles of a pair of mating gears.
• 
  
• Common tangent: The line tangent to the pitch circle at the pitch point.
• 
  
• Base circle : An imaginary circle used in involute gearing to generate the involutes that form the tooth profiles.

·         Line of Action or Pressure Line: The force, which the driving tooth exerts at point of contact of the two teeth. This line is also the common tangent at the point of contact of the mating gears and is known as the line of action or the pressure line. The component of the force along the common tangent at the p point is responsible for the power transmission.

The component of the force perpendicular to the common tangent through the pitch point produces the required thrust.

·         Pressure Angle or Angle of Obliquity (φ): The angle between pressure line and the common tangent to the pitch circles is known as the pressure angle or the angle of obliquity.

For more power ‘transmission and lesser pressure on the bearing pressure angle must be kept small. Standard pressure angles arc and 25°. Gears with 14.5° pressure angles have become almost obsolete.

·         Path of Contact or Contact Length: Locus of the point of contact between two mating teeth from the beginning of engagement to the end is known as the path of contact or the contact length. It is CD in the figure. Pitch point P is always one point on the path of contact. It can be subdivided as follows:

Path of Approach: Portion of the path of contact from the beginning of engagement to the pitch point, i.e. the length CP.

Path of Recess: Portion of the path of contact from the pitch point to the end of engagement i.e. length PD.

·         Arc of Contact: Locus of a point on the pitch circle from the beginning to the
end of engagement of two mating gears is known as the arc of contact in fig. 3.22, APB
or EPF is the arc of contact. It has also been divided into sub-portions.

Arc of Approach: It is the portion of the arc of contact from the beginning of engagement to the pitch point, i.e. length AP or EP.

Arc of Recess: Portion of the arc of contact from the pitch point to the end of engagement is the arc of recess i.e. length PB or PF.

·       Angle of Action (δ): It is the angle turned by a gear from the beginning of engagement to the end of engagement of a pair of teeth i.e. the angle turned by arcs of contact of respective gear wheels. Similarly, angle of approach (a) and angle of recess (β) can be defined.

S=a+ β

Machine Design (Gear Drive) (7)

Machine Design

Gears

Gear drives offer following advantages over the chain or belt drives: 

(1) It is a positive drive and the velocity ratio remains constant.

(2) The center distance between the shafts is relatively small, which results in Compact construction.

(3) It can transmit very large power which is beyond the range of belt or chain drives.

(4) It can transmit motion at very low velocity which is not possible with the belt drives.

(5) The efficiency of gear drives is very high up to 99% in case of spur gear.

(6) A provision can be made in the gearbox for the gear shifting, by just changing the velocity ratio over a wide range. 

Disadvantages : 
(1) The gear drives are costly and the maintenance cost is also very high.
(2) The manufacturing process for gears are complicated and highly specialized.
(3) Gear drives require careful attention for lubrication and cleanliness.
(4) Gear drives also requires precise alignment of the shaft.